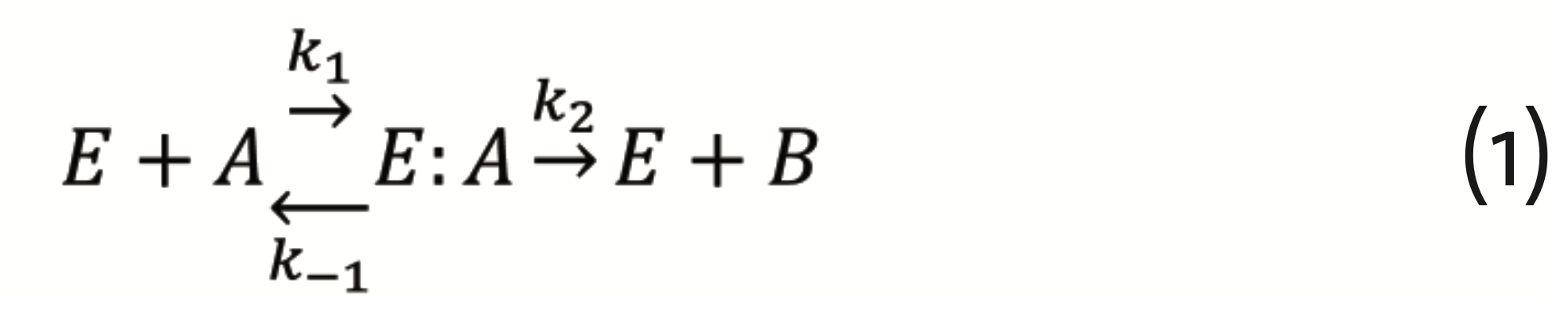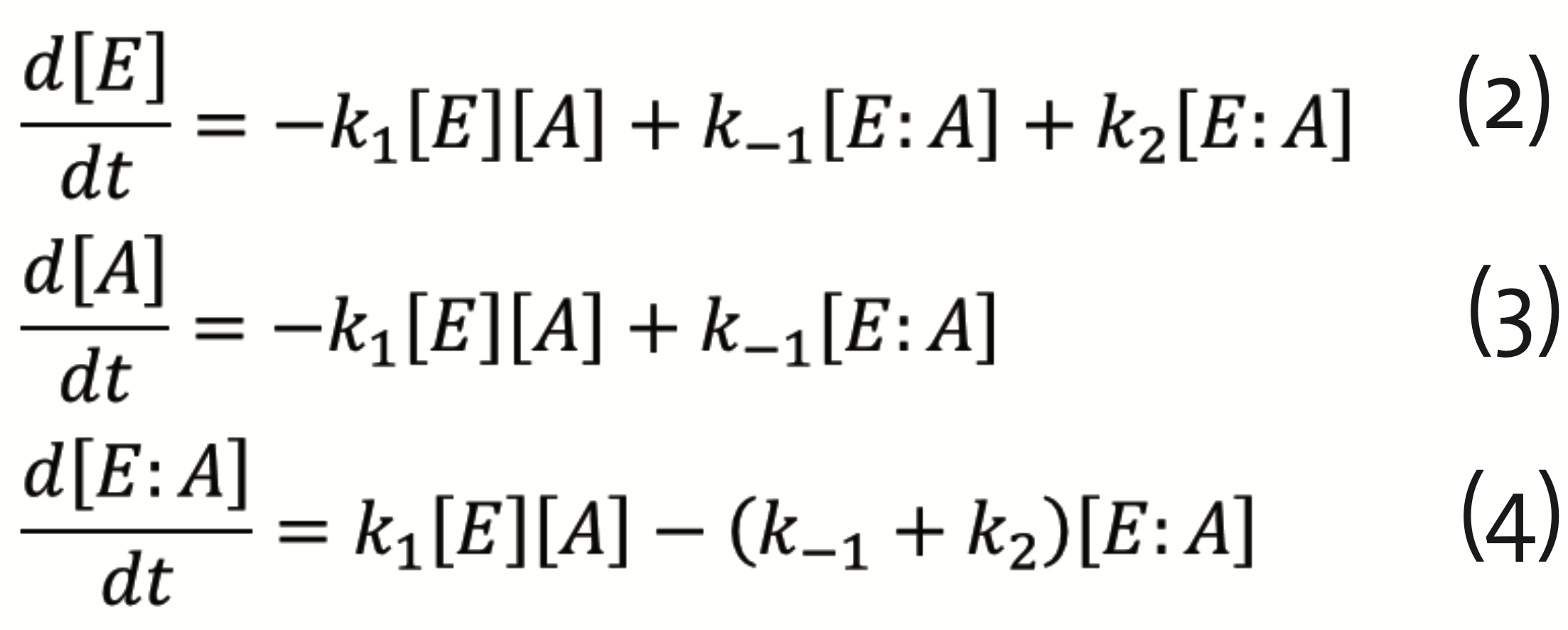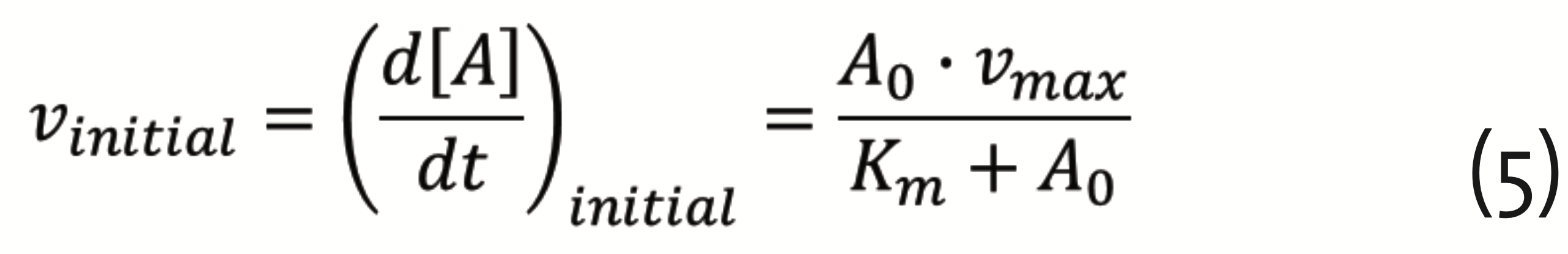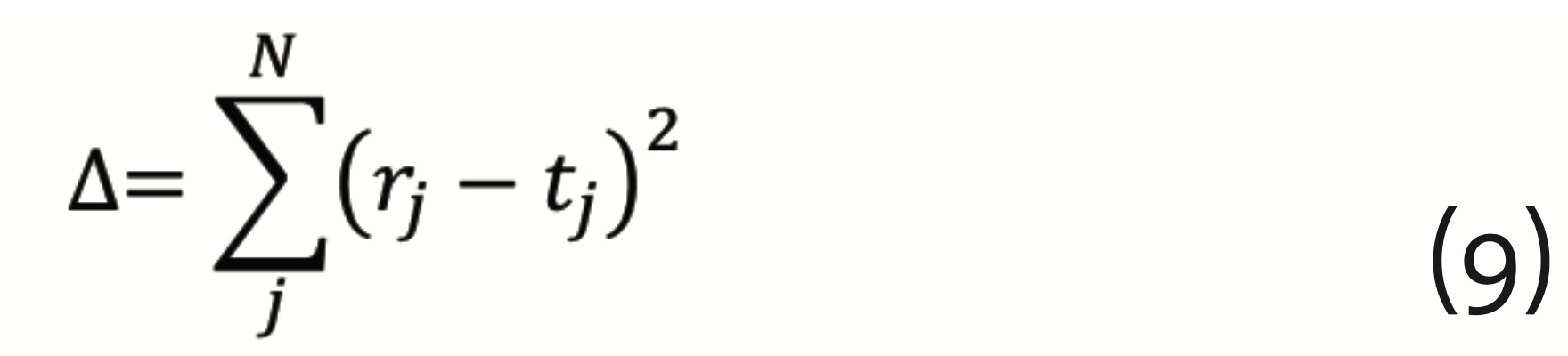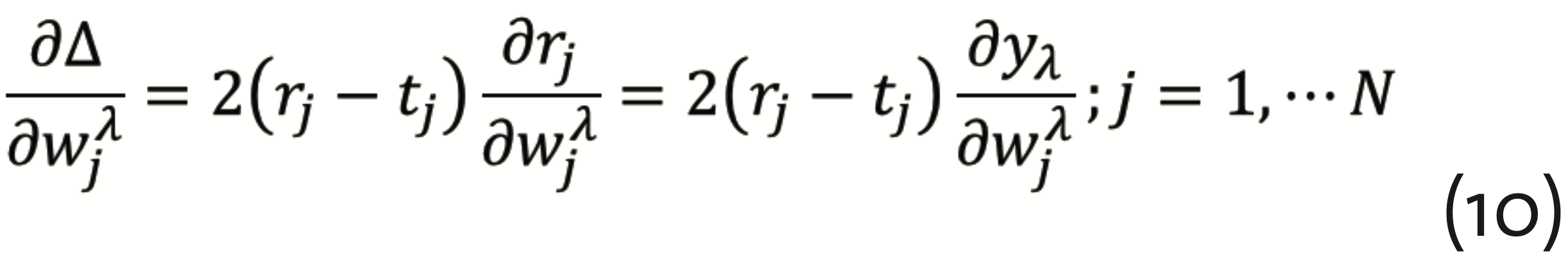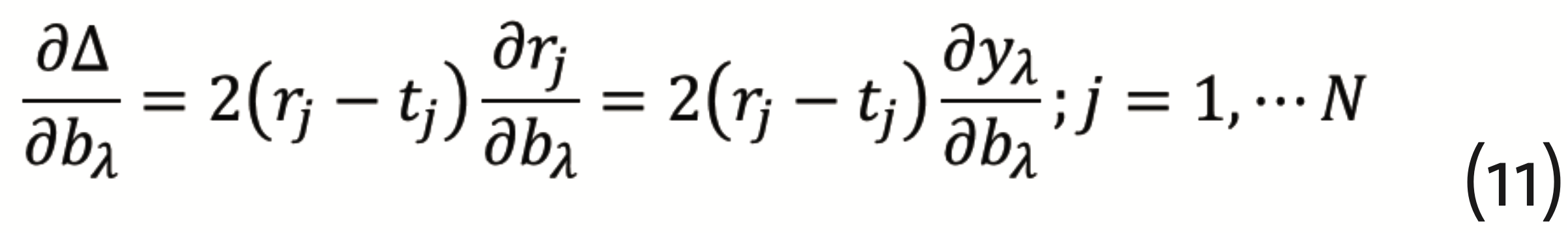Quantitative biology – a perspective for the life sciences’ way into the future
Abstract
Life science research and life sciences’ industries are facing an overwhelming complexity of biology. Today’s scientific methods and technologies allow for a very detailed look at biology. What is left to do, is understanding and interpretation. Quantitative biology, the close coupling of life sciences, mathematics, and statistics is likely to provide the methodologies to turn collected data into dedicated information and knowledge. The most promising approach is the formulation of mathematical models on the basis of machine learning. The predictive power of such an approach is a promising option for basic biological research, medicine, pharmacology, agricultural science, and ecology. Furthermore, also R&D of related life sciences industries can take advantage of this digital approach to meet future challenges and market requirements. Quantitative biology plays the role of an enabling technology.
1 Introduction: biology as a quantitative science
It is clear that today biology is influencing human thinking, perception, and action in an increasing number of different ways. The 21st century is seen as the century of biology (Venter and Cohen, 2004). Life sciences’ historical route from genetics to genomics, now approaching and establishing synthetic biology shows its impact, not only on biological basic research, but also on the different disciplines of biotechnology, medicine, pharmacology, and last but not least, agricultural science. Consequently, there is a corresponding influence on the life science industry, including pharmaceutical industry, diagnostic industry, medical product industry, food as well as dietary supplement industry, and agricultural industry.
In a more general view the combination of biology, statistics, and mathematics has been termed quantitative biology (Zhang, 2013). The notion of quantitative biology may sound a little bit unfamiliar today. We are rather used to talk and hear about bioinformatics, computational biology, biometry, biostatistics, biomathematics, and similar disciplines, all of which share the combination of biology with some other scientific discipline, which is related to calculation, modeling, and computing. Though in the past, biology itself has been recognized as a predominantly descriptive science (Mayer, 1997), the roots of a quantitative view are fairly old, as can be seen in the proceedings of the first Cold Spring Harbor Symposium on Quantitative Biology, which Reginald Harris organized in 1933 (Witkomski, 2018). This may be seen as a reaction to the early 20th century discussion about biology as an autonomous science, or just a sub-discipline of physics and chemistry (Mayer, 1997).
Today, biology has established as a science of information, driven by molecular biology, genetics, and genomics. Functional genomics, as well as metabolomics have produced data that demonstrate the existence and importance of complex pathways and networks in living cells and organ- isms. The complexity of biological systems appears to be much higher than in today’s technological implementations, which has become evident in applying, e.g. non-equilibrium thermodynamics, synergetics, and chaos theory (Haken, 1983) to biological phenomena. Hence, it is not at all surprising that advanced methods of mathematics, statistics, and information theory are becoming routine tools in biology (Green et al., 2005), as well as in the related sciences medicine, and agricultural change of view in biology, which is characterized by growing popularity of the notions of network and ecosystem, even beyond neuroscience and microbiology. Not only do biologists nowadays talk about systems biology (Ideker et al., 2001), but also systems (bio)medicine (Lenoir, 1999)(Liu, 2010)(Ayers, 2015)(Maurya, 2010) has become an emerging concept in medicine, pharmacology, and diagnostics (Abu-Asab, 2011).
2 An owerview of quantitative biology
At the beginning of the 20th century, quantitative biology was applied to only a few particular problems, mainly in two different areas, pharmacology on the one hand, and breeding of plants and animals on the other hand.
2.1 Enzyme kinetics
As for pharmacology, probably the first mathematical model of quantitative biology was the Michaelis-Menten theory of enzyme kinetics (Michaelis and Menten, 1913) (Cornish-Bowden, 2013) (Cornish-Bowden, 2015). Decomposing an enzyme’s E reaction with a substrate A into the steps of substrate binding, reaction catalysis, and product B release (Schnell, 2014)
which can be described by the set of differential equations for E, A, and their complex E:A
The corresponding equation for the reaction rates (Michaelis-Menten equation) reads (Pinto and Martins, 2016)
with A0 the initial substrate concentration, vmax = k2∙E0 , E0 the initial enzyme concentration, and Km = (k-1+k2)/k1, the Michaelis constant. The theory developed by Michaelis and Menten, provided the foundation for quantifying physiology and pharmacology (Dost, 1953). It plays an important role in drug development, still today.
2.2 Quantitative genetics – the breeders’ equation
Following the ideas of Darwin and Mendel, people tried to understand and started to predict, thereby optimizing, breeding of plants and animals on the basis of the so-called breeder’s equation (Lush, 1937) (Ollivier, 2008). This simple equation allows to estimate the change (response ∆Z) in occurrence of a particular quantifiable trait in the
off-spring generation due to selection for this trait in the parent generation. h2 is called the heritability, S is the so-called selection differential, which represents the difference of a trait’s average value in the respective whole population and the average value in the selected subpopulation. Remarkably, this equation is independent of molecular genomic details, which is the basis for its present-day role in theoretical genomics (Visscher et al., 2008). It should be noted that this early mathematical model being used in quantitative biology, had commercial applications from its very beginning.
2.3 Bioinformatics
The impressive development of DNA, RNA, and peptide sequencing that we see today, was possible only through the collaboration of three disciplines, bioinformatics, computer technology, and sequencing technologies. Bioinformatics provided the mathematical and statistical tools to structure, analyze, and annotate biologically, what had been produced with sequencing machines. High-performance computers were needed, to handle and process the related data, which still today is the core of bioinformatics.
2.4 Molecular phylogeny
Many authors see the actual initialization of bioinformatics in a paper about molecular evolution by Emile Zuckerkandl and Linus Pauling (Zuckerkandl and Pauling, 1962) (Zuckerkandl and Pauling, 1962b) (Zuckerkandl and Pauling, 1965). They recognized the relationship between sequence variation and evolution, defining the foundations of phylogeny, a methodology, still popular today (Lemoine et al., 2018) in sophisticated versions as probabilistic models of evolution.
2.5 Sequence analysis: comparison, alignment, and pattern recognition
The key aspect of sequence analysis is comparison (Pearson and Lipman, 1988) to find and quantify similarity in sequences and accordingly in function. In the beginning, this was based on alignment, the most important methods being the Needleman-Wunsch algorithm (Needleman and Wunsch, 1970) for global alignment and the Smith-Waterman algorithm (Smith and Waterman, 1981) for local alignment. The complications arising from sequence insertions, deletions, and mutations can be managed by statistical scoring systems, which bear some analogy to the concept of entropy in information theory (Altschul, 1991). Thus, scoring not only takes into account identities, but also homologies, i.e. sequence elements, which could be exchanged “easily” in the course of evolution without loss of function, and therefore can be classified as being equivalent. With the growing size of sequence databases, more efficient algorithms, which computationally are less demanding, have been formulated. The most popular one today is the BLAST algorithm (Altschul et al., 1990), providing a quantitative measure for sequence homology in terms of the so-called expectation value (E-value), which is the probability of the respective alignment being purely by chance. The lower the E-value, the more significant is the homology.
Based on pairwise alignment, algorithms for multiple sequence alignment have been developed. From the comparison of a set of DNA or peptide sequences they can generate what is called a consensus sequence, i.e. stretches of sequence that are identical or closely related, while other ranges of the sequences differ more or less significantly by mutations, insertions or deletions. The most widely used software systems today are the different versions of CLUSTAL (W and X) (Larkin et al., 2007).
2.6 Pattern recognition in sequence analysis
An important result of sequence comparison is the identification of sequence pattern, which typically provide two kinds of information. Firstly, common, i.e. evolutionary conserved patterns indicate phylogenetic relationships (Fitch and Margoliash, 1967) in a quantitative manner. Secondly, sequence pattern can be correlated with genetic and molecular function. To this end, starting from classification and clustering, algorithms for pattern recognition have been developed (de Ridder et al., 2013). These algorithms also paved the way into machine learning (Baldi and Brunak, 2001) and big data, which was achieved by introducing probabilistic frameworks for the respective models. Building statistical models on the basis of existing data bears a lot of uncertainty, which makes the difference between inference and deterministic conclusion. In statistics, there two different philosophies considered, the Fisher philosophy, also called the frequency approach, and the Bayes philosophy, using prior and posterior distribution knowledge (Leonard and Hsu, 1999), in other words conditional probabilities. It has been shown that Bayesian methods are the most appropriate approach for modeling of biological systems, because it readily allows analyzing data against the background of their actual biological context (Gupta, 2012).
2.7 Some Remarks on Machine Learning
Machine learning is an important aspect of arti- ficial intelligence (Carbonell et al., 1983). The origin of machine learning goes back to the late 50s. It was characterized as a ” … field of study that gives computers the ability to learn without being explicitly programed” (Samuel, 1959). It is seen as the right choice for solving problems that cannot be tackled by pure computing. This, of course, is not only of interest for the life sciences. The financial industry is using machine learning (Mark et al., 2018) for management of the risks in stock market trading and credit issuing (Fagella, 2018). Furthermore, it is also used in marketing (Chow, 2017), for numerous popular web services (Luckow et al., 2017), in manufacturing, energy production, as well as for automotive, public transport, and aviation maintenance prediction (MathWorks, 2018).
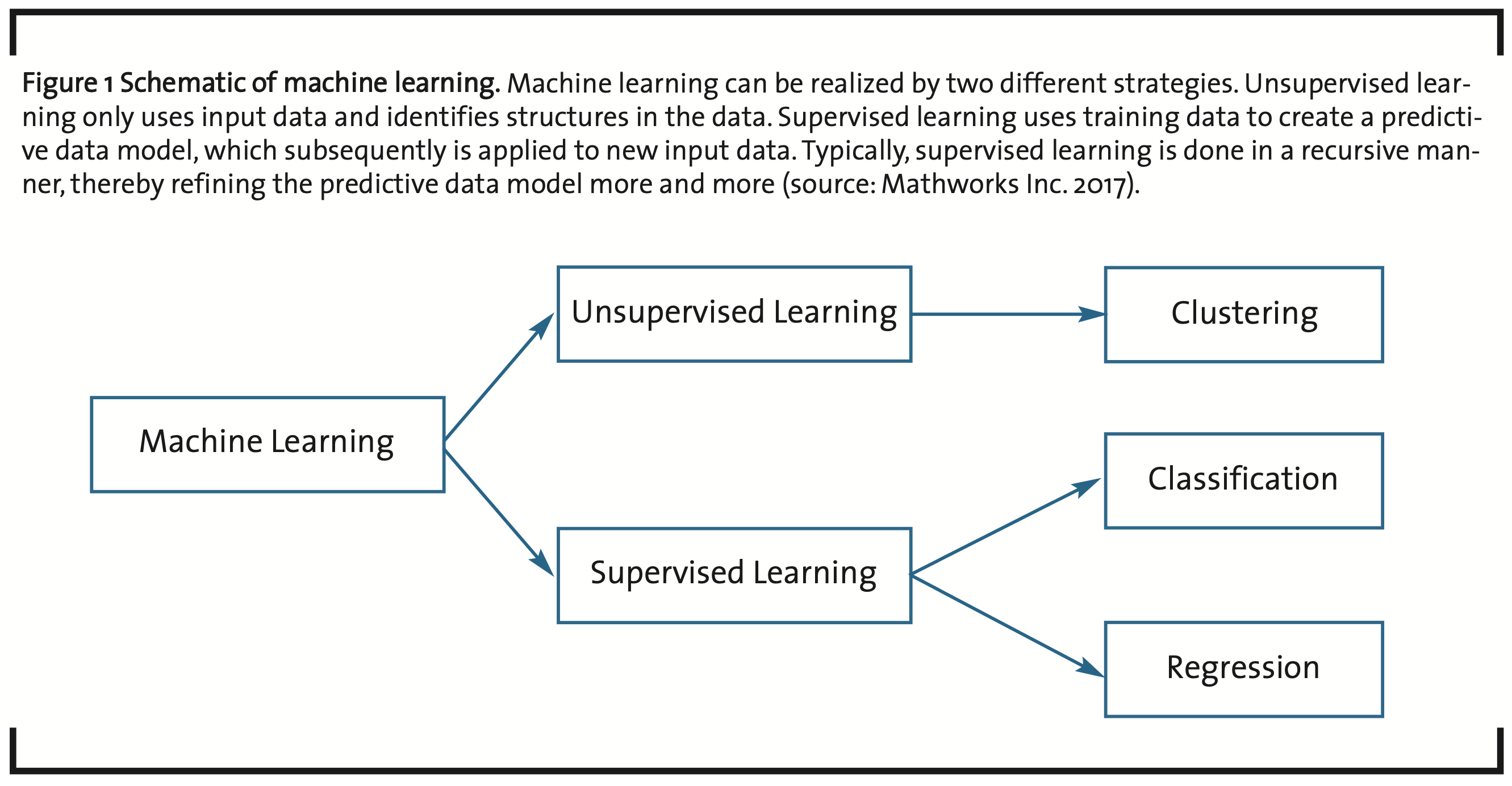
The most important method in what is called unsupervised machine learning is clustering (Filippone et al., 2008), i.e. distinguishing and grouping elements into subsets of a given set of input data based on a measure of similarity applied to the characteristic features of the elements (see fig. 1). With respect to post-processing, this is a divide-and-conquer strategy, because the overall size of a data analysis challenge can be split into analyzing a number of subsets.
Supervised learning is based on experience, i.e. data analyzed for training a particular statistical model obtained through clustering, classification and regression. New input data can then be processed by the trained, predictive model to generate new information. This is done typically in a recursive manner to optimize the parameters of the predictive model.
In general, machine learning is used for data-driven applications and hence requires enormous computing power. For many successful applications, two technological infrastructure innovations have been very important, cloud computing and the involvement of graphical processor units in so- called GPU computing.
2.8 Hidden Markov models
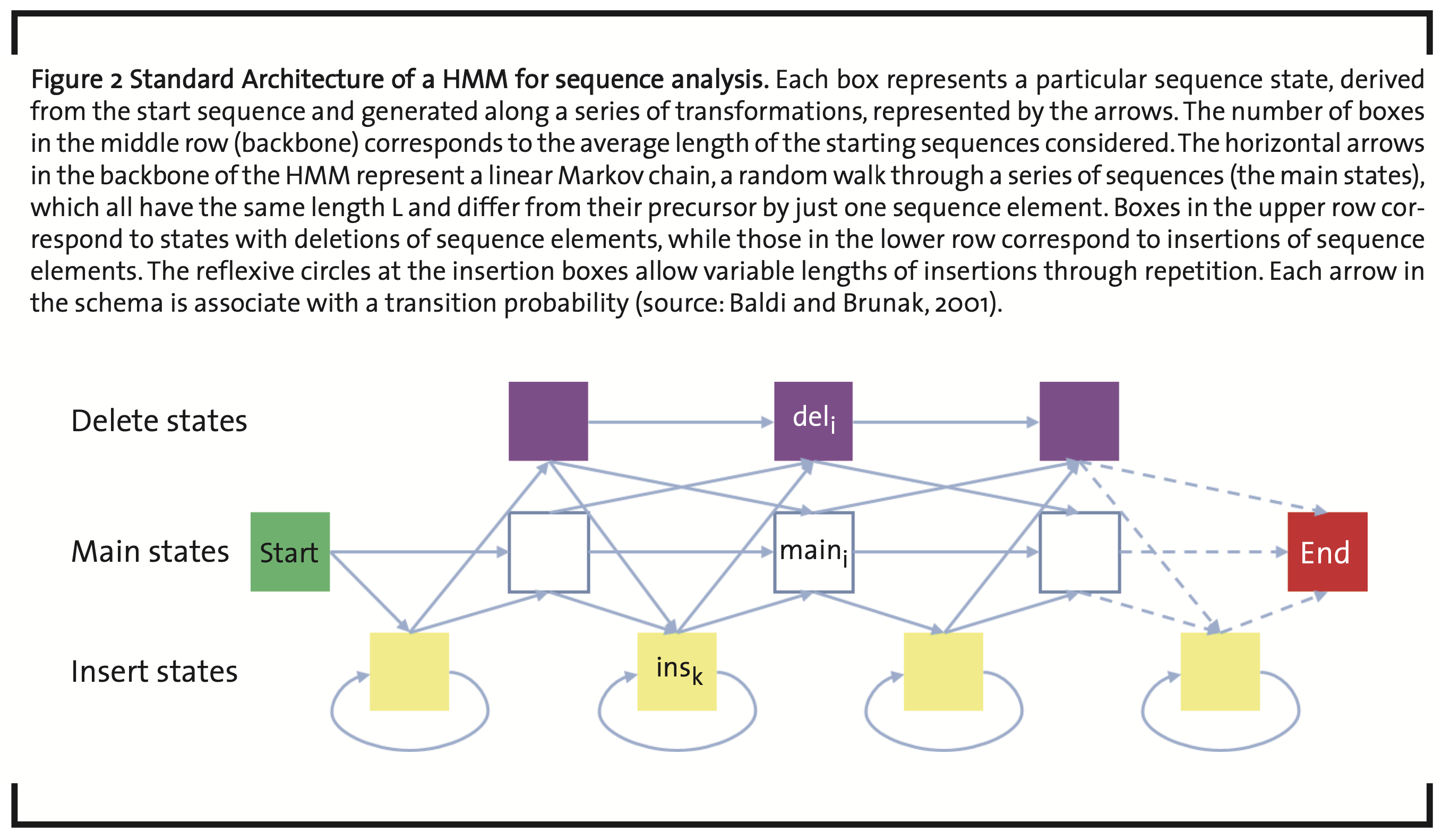
An important machine learning methodology in quantitative biology is realized by so-called Hidden Markov Models (HMMs) (Baldi and Brunak, 2001b). They are tools to analyze serial data like, e.g. time series or biological sequences. In the comparison of sequences (Krogh, 1994), they are used to find relationships between sequences by a probabilistic random walk through a series of states in sequence space (Markov chain). Depending on the selected parameters, new states are either accepted or rejected. Starting from an initial sequence, intermediate sequence states are generated by transitions generated by local repetition, mutation, insertion, and deletion of sequence elements (Fig. 2). Sequence elements can be nucleobases and amino acids, but also sequence pattern like, e.g. base triplets or higher multiplets, amino acid pattern characteristic for a particular folding or function. Accordingly, there are specific transition and emission parameters for sequence elements. In terms of Bayesian probabilities, this gives a quantitative measure of relatedness with respect to the section of the sequence space, reached by the Markov chain.
Usually, a set of reference sequences is taken to train the model and generate its parameters (Rasmussen and Krink, 2003). After optimization the set of parameters obtained in the individual main and intermediate states carry important information about the sequences involved. Typical applications are the identification of coding areas and protein binding sites of DNA strands.
It should be noted that Hidden Markov Models are also used in speech recognition, optical character recognition, and industrial process control (Windmann et al., 2016). Furthermore, due to their layered structure, Hidden Markov Models are closely related to, or may even be seen as a special case of so-called neural networks, actually one of the most important concepts in machine learning.
2.9 Artificial neural networks, convolutional neural networks, and self-organizing maps
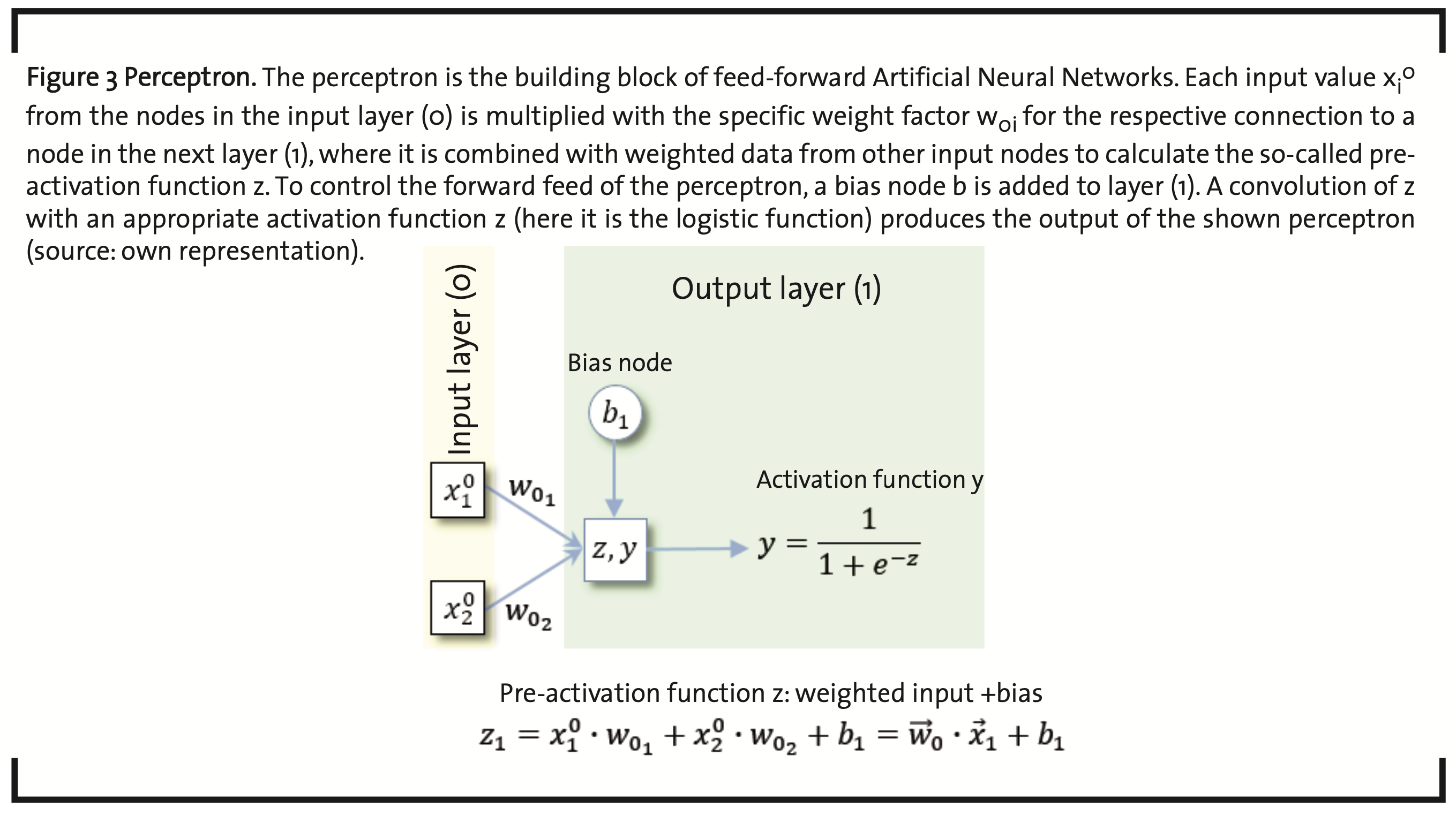
As the name already indicates, artificial neural networks (ANNs) have their origin in the attempt to simulate and understand the characteristics of biological neurons. The human brain is assumed to consist of about 100 x 1012 neurons (Herculano-Houzel, 2009) and about ten times as many glial cells, involved in a large number of specific net- works by synaptic connections. On arrival at the synapse which is formed by an axon terminal of the emitting neuron and a dendrite of the receiving neuron, and often coupled to a glial cell, the electrical signal is transferred by neurotransmitters and, may be maintained, enhanced, attenuated, or averaged over several signals in the postsynaptic neuron. This behavior has been modeled by so-called perceptrons (McCulloch and Pitts, 1943) (Rosenblatt, 1958) (Stansbury, 2014) (Stansbury, 2014b) (Fig. 3).
Each input value xjλ-1 in the input layer (λ-1=0) is multiplied with a weight factor wjλ specific for the connection to a node in the next layer λ. In each node, the incoming weighted data items are summed up and can be modified by the parameter bλ of a so-called bias node. The expression
is sometimes called the pre-activation function of the signal and is the summation over all data items coming in from all the nodes of the previous layer. The actual activation function is typically a convolution to normalize z to the interval [0,1], which is achieved, e.g. by the sigmoid logistic function
The value of yjλ calculated in each node of the the next layer(yjλ→xjλ+1)(Fig.4).
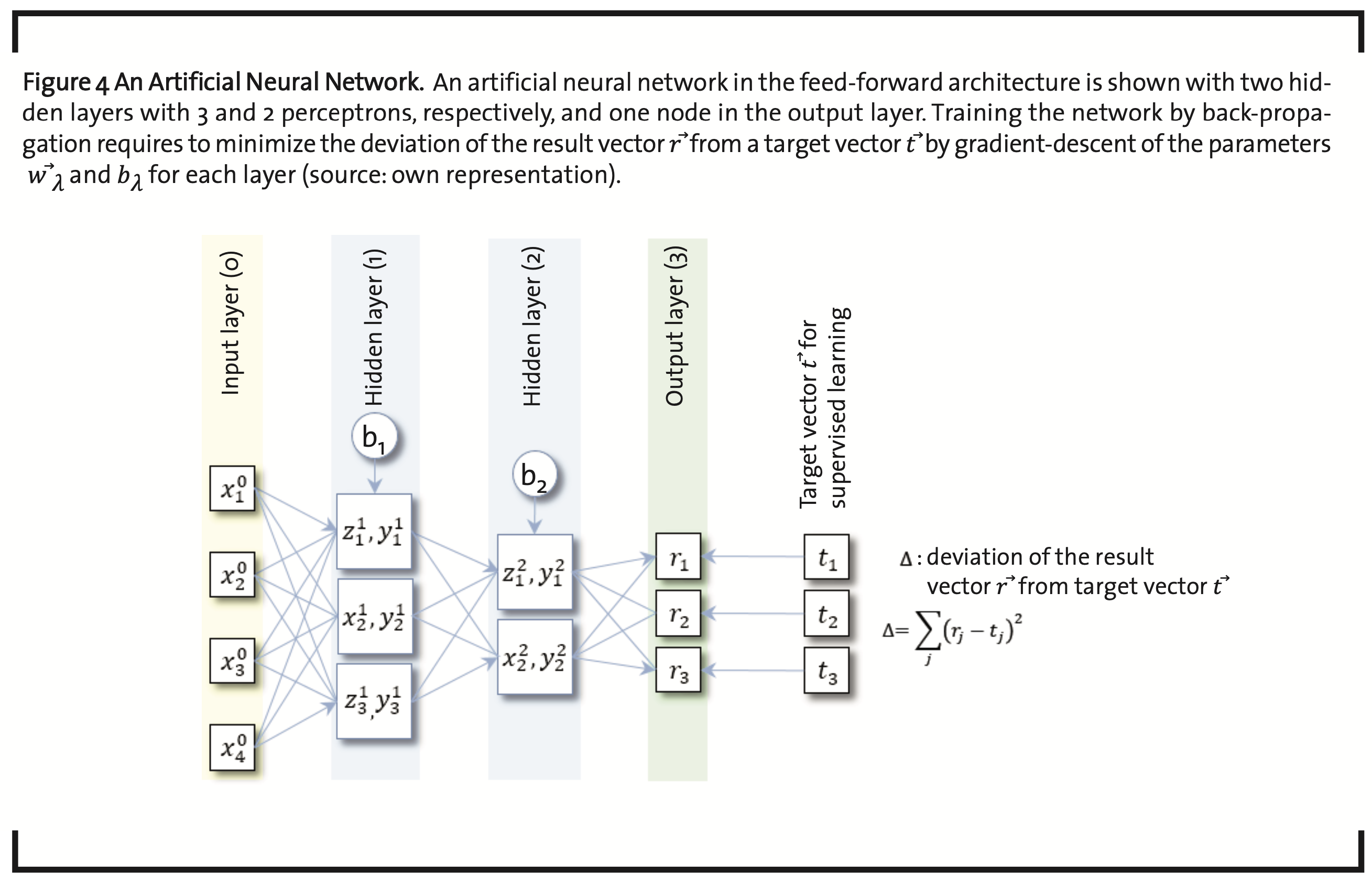
According to the nature of the problem and the kind of data available, the number of nodes per layer can vary. Each node in layer λ-1 is connected to each node in the next layer λ, and every data item of a given layer is send to all nodes in the successive layer and multiplied with a weight factor, specific for the particular connection. Accordingly, the number of parameters in an ANN is of the order of N∙L, with N the average number of nodes per layer and L the number of layers.
Parametrization of ANNs is usually subject to supervised learning. An input vector x⃗ is taken together with an initial guess of the parameters.
{π=(w⃗λ ,bλ),1≤λ≤L} and {bλ,1≤λ≤L} and the output vector of the final layer r⃗ is calculated. The output is compared to a vector of target values t⃗. The difference
has to be minimized, which can be achieved by the so-called gradient descent method with back propagation. This requires to calculate the gradients
and
from which corrections for the respective layer can be determined. Back propagation means that, beginning with the output layer, this procedure has to be repeated for each anterior hidden layer. It should be noted, however, that the gradient descent method is subject to the multiple minima problem. Together with the substantial number of necessary parameters, this is rendering ANNs computationally demanding. Even though, ANNs have a really wide spectrum of applications in science (Musib et al., 2017), medical diagnosis (Kononenko, 2001)(Shen et al., 2017) (Ting et al., 2018), and the industrial context (Lennox et al., 2001).
Recent developments in the field of ANNs go beyond the feed forward architecture. To allow for more flexibility, the number of hidden layers has been augmented. In addition, so-called convolutional neural networks (CNNs) have dropped the restriction of forward transfer and also include connection between nodes within a layer and loops around nodes. The advantage is in the possibility to analyze the data in a hierarchical manner, which is very helpful in image processing and text analysis. Furthermore, CNNs can be used in an unsupervised learning mode (Radford et al., 2016). Working with multi-layered ANNs and CNNs is often called deep learning and has become an integral part of the software infrastructure of many web portals (Hern, 2016) (Abdulkader et al., 2016). It is also the basis of what is called predictive analytics (Siegel, 2016), a methodology that is likely to gain enormous influence on web-based business models. Even though, however, impressive progress in handling complexity has been made, the level reached today is still negligible compared to the complexity of the human brain (Koch, 2012).
Another type of neural networks is the self-organizing map (SOM), which has been inspired by the relationship between an image on the eyes’ retina and the corresponding areas in the visual cortex of the brain. Accordingly, SOMs seek to map a dense or contiguous high-dimensional input space to a discrete low-dimensional output space (Kohonen, 1958), thereby compressing information. SOMs belong into the class of non-supervised learning neural networks. In practice one takes a set of nodes representing the input data, the input layer, and maps it to another set of nodes, the computational or output layer. Consequently, the assignment of input nodes to computational nodes is based on competition and collaboration between the computational nodes. In an iterative procedure, the weights and interaction parameters of the individual computational nodes are adjusted to enhance vicinity to the input nodes based on a (projected) distance criterion. Typical applications are the optimization of trajectories for robots (Stergiopoulos, 2012), language recognition, signature recognition, face recognition, seismic data analysis, engineering (Simula et al., 1999), and industrial process control (Frey, 2012). In addition, SOMs have also been used in computer-assisted drug design (Reker et al., 2014) for drug target profiling.
2.10 Computer-assisted molecular design and biomolecular structure prediction
The use of computers in visualizing three-dimensional molecular structures dates back into the 1980s years (Frühbeis et al., 1987). Quantitative structure-activity relationships based on the comparison of molecular structures and their physical, chemical, biological, pharmacological and toxicological properties have been used to design and develop new chemical entities for the respective purposes, ever since (Schneider and Fechner, 2005). Later on, this has been complemented by methods of computer-assisted synthesis planning (Hoffmann, 2009). In parallel, sophisticated algorithms have been developed, which are able to predict the structure of biopolymers. A particular challenge is the assessment of folding and self-organization of the molecules. In principle, so-called ab-initio prediction of structures is possible, but computationally very demanding. The requirements of accuracy of the necessary parameters are enormous. Other approaches start from the prediction of secondary structure elements, whose self-organization is then searched to complete the structures. Quite successful are pragmatic methods, which predict structures on the basis of sequence homology to biopolymers with known tree-dimensional structures (Krieger et al., 2003). The large amount of structures (140591) (RCSB PDB, 2018) published in the RSCB Protein Data Bank (Berman et al., 2018) obtained by x-ray crystallography, multi-dimensional NMR measurements, neutron scattering, and cryo-electron microscopy support this approach significantly. Due to its convenience, homology modeling is widely used in the research and development departments the pharmaceutical industry for what is called structure-based or rational drug design. Drug target structures are used for so-called in-silico screening, which is a computational method of estimating target affinities and rate drug candidates, before they have been synthesized. It can be seen as an option to reduce the amount of chemical syntheses necessary for the development of new drugs (Caldwell, 2015).
2.11 Modeling of biological systems
An important branch of quantitative biology is the modeling of biological systems (Gunawardena, 2014). The targets of modeling range from molec- ular aggregates to pathways, to cells, to organisms, and populations. The phenomena considered comprise, e.g. material and heat flux balance, metabolic flux analysis, and population dynamics (Shimizu and Matsuoka, 2015). The challenge, but also the motivation, is in modeling and thereby improving comprehension of biological systems’ inherent complexity, a situation, also envisioned in medicine (Harz, 2017).
There are basically four different directions in biological systems’ modeling. These are (i) the mechanistic modeling of processes at various levels, (ii) the deterministic simulations, using methodologies originating from many-particle physics and fluid-dynamics, (iii) artificial neural and other networks, and (iv) models based on virtual reality, which, by means of man-machine interfaces are supporting human activities and interventions to biological systems.
2.12 Mechanistic modeling and kinetic biological models
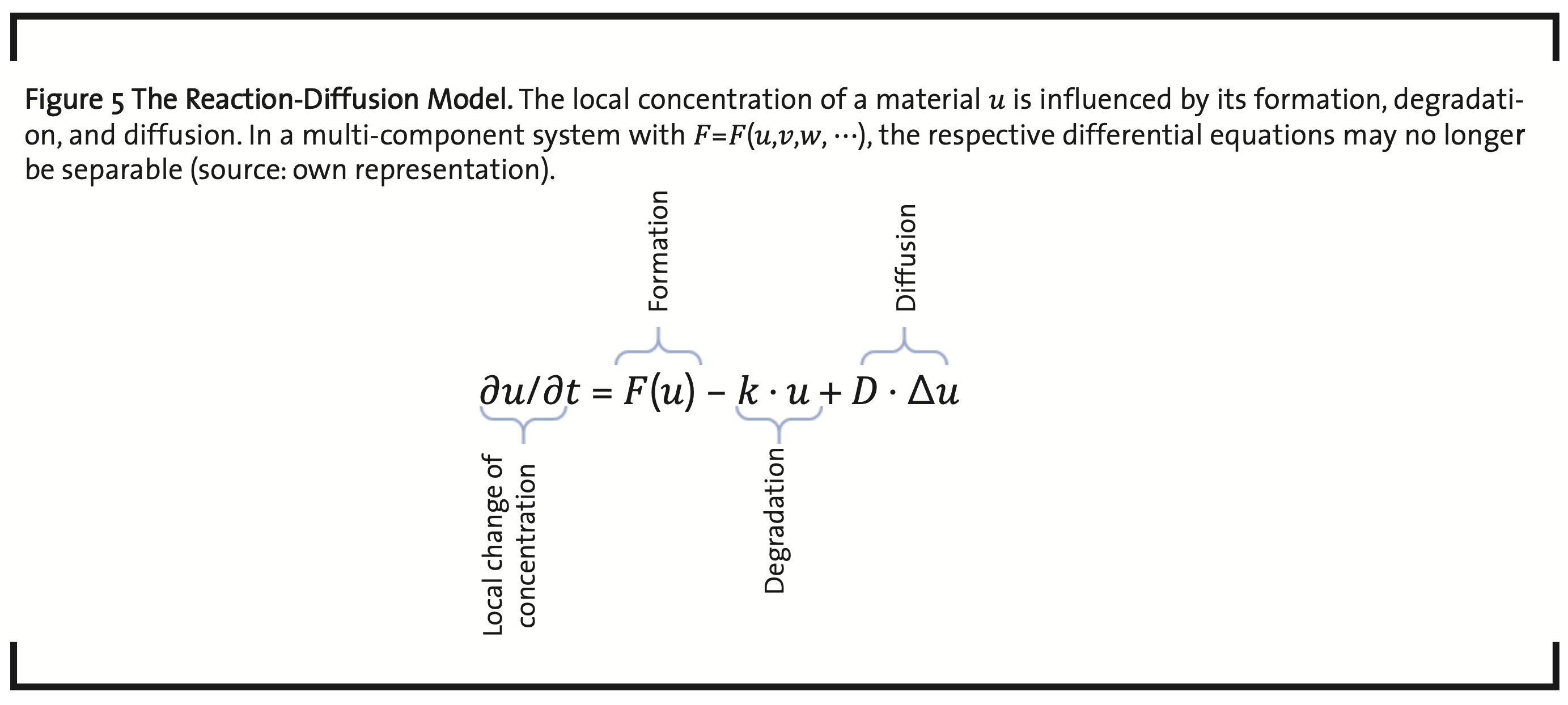
The dynamics of a biological system has two aspects, internal dynamics and the interaction and exchange with the system’s environment. On a cellular level, this comprises signaling, metabolism, and material transportation. In addition, there is the dynamics of growth, regeneration, and replication, at cellular and organismal level (Chara et al., 2014). Models used in this context are usually systems of ordinary differential equations (ODEs). Examples are kinetic models, and reaction-diffusion models (Britton, 1986) (Volpert and Petrovskii, 2009), also named Turing models (Turing, 1952), which are the most important models to represent the dynamical behavior of living systems (Raue et al., 2013). The dynamics of pattern formation (Kondo and Miura, 2010) and wave propagation, e.g. in signal transduction, gene expression (Gaffney and Monk, 2006), tumor growth, and population growth, can be modeled on the basis of equations like shown in Fig. 5.
A versatile open source software system for building and analyzing such kind of models is MOR- PHEUS (Starruß et al., 2014).
2.13 Deterministic and stochastic modeling
In combination with simulations of the time evolution, deterministic models, which have been developed for molecular or particle dynamics (Vlachakis et al., 2014), and fluid dynamics are used to study, e.g. the system’s response to perturbations (Marshall, 2017). For mechanical systems, deterministic models are based on equations of motion that describe the dynamics of the system modeled. By simulation, one obtains a trajectory, document- ing the time evolution of the model under the given conditions. Stochastic methods are used for systems with significant noise, which can be represented by random fluctuations. Typical examples are populations (Sharkey, 2011), whose size fluctuates due to death and reproduction.
Rather than looking at a definite trajectory, the Monte-Carlo method (Frenkel, 1990) can be used for scanning the models’ phase space by an appropriate random walk, to guarantee ergodicity of the scan. Monte-Carlo methods are often used for high-dimensional systems with many internal interactions.
2.14 Probabilistic biological models
Data-driven biological models are used at all biological levels. For problems that are not clearly deterministic, like establishing relationships between molecular interactions, genetic predisposition, and physiology, models based on Bayesian statistics like HMMs are preferred also in medicine (Couzin, 2004). There are numerous initiatives to take what is called computational medicine to the clinic (Winslow et al., 2012). Models at population level are of particular interest in epidemiology and public health surveillance (Zhang et al., 2013).
2.15 Modeling biological networks
Inside living cells, there are two kinds networks, the network of molecular interactions and the genetic network of genes. While the network of molecular interaction is the physical backbone of cellular functions, the genetic network is an infor- mation network (Sharan and Ideker, 2006). Like the genetic code itself, both networks underlie evolutionary changes, and homology of networks is valuable information, e.g. in the field of synthetic biology and in the design of molecular machines. On the basis of graph theory (Friedman, 2004), these networks serve to visualize and structure data of gene expression (Liu, 2018), proteomics, and metabolism. They are the basis for information resources and simulation models for signaling as well as metabolism of cells. Examples are the E_CELL system for generic cell simulations (Tomita et al., 1999), the EcoCyc system (Keseler et al., 2009) for Escherichia coli, and the BioCyc system (Karp et al., 2017) comprising Bacillus subtilis, Saccharomyces cerevisiae, and Homo sapiens (Romero et al., 2004).
2.16 Biological models for virtual and augmented reality
Virtual reality is based on image data in combination of hardware for graphical display, audio, and hardware for haptic interaction and control. Together, this is an example of a man-machine interface and has its roots in flight simulators. But the use of virtual reality has a long tradition also in medicine (Kaltenborn, 1993). It is nowadays well established for surgical education and training (van der Meijden and Schijven, 2009), and also applied in the recovery of stroke patients (Laver et al., 2012) (Henderson et al., 2007) and general traumatic brain injury (Zanier et al., 2018). The underlying data are partly based on geometrical models and partly on photographic images, which, after appropriate image processing are merged with the mathematical model.
Augmented reality is the combination of real-time visual perception with data and information from other sources. A typical example is the head-up display in aircrafts and cars. Information, which usually is not visible while looking out of the front window is projected on the window overlaying the view through the window. This principle is used, e.g. in liver surgery. The problem of liver surgery is related the complex vascular networks of this organ, which can easily be destroyed by surgical interventions, e.g. to remove a tumor, or in liver transplantation. Software systems have been developed that are able to generate a geometrical model of a patient’s liver from magnetic resonance tomogra- phy (MRT), x-ray computed tomography (CT), positron emission tomography (PET), or ultrasound tomography. The visualized geometrical model of the liver can be used to plan the surgical intervention (Reitinger et al., 2006), and in real-time to support surgeons by projecting the blood vessels onto the surface of the organ (Christ et al., 2017).
3 The present situation
Even though, in the course of the last two centuries, scientists have accumulated a plethora of biological observations, data, and knowledge, numerous open questions and uncertainties are still left (Levin, 2006) (Adams, 2013). Hence, to advance life sciences and its applications, and exploitations, many experts see the necessity of interdisciplinary collaborations of biologists, statisticians, and mathematicians (Hastings, 2005) (Heffelfinger et al., 2004), which actually is the core of data-driven quantitative biology. It is important now, to enable and support such collaborations, not only for academic research, but also for life sciences industries’ research and development. It should be noted, however, that such collaborations are not trivial, due to differences in terminology and methodology (Ledford, 2015). In other words, progress based on data and innovative methods, is not an automatism. The way has to be paved (Bialek and Botstein, 2004).
4 Future options for medicine and the healthcare industry
The pharmaceutical industry is in a difficult sit- uation. Therapeutic medical interventions, including medications, can be curative, or can serve for disease maintenance. But they can also be just palliative, if the stability of a patient’s status cannot be maintained any longer. In recent decades, this has been a comfortable situation for the pharmaceutical industry in that drugs were administered for an ever-increasing time span between initial diagnosis of an indication and the death of the patient.
The growing financial burden emerging from healthcare systems all over the world (Cunningham, 2010) (Dickman et al., 2016), however, has provoked criticism of the pharmaceutical industry’s business model (PriceWaterhouseCoopers, 2009) (Tyson, 2015). In addition, reimbursement of new drugs that the pharma industry is bringing to the market, is more and more coupled to proven superiority with respect to drugs already on the market. Furthermore, agreements on outcome-based reimbursement between pharmaceutical companies and health insurances are becoming more and more common. This puts the pharmaceutical industry under enormous innovation pressure (Taylor, 2015)(Thakor et al., 2017), in particular against the background of difficulties in feeding the R&D pipelines and attrition rates of 80-90% on the way to approval (Caldwell, 2015)(Elsevier white paper, 2017). On the long term it is clear that the pharmaceutical and healthcare industry cannot just continue to optimize existing methodologies and processes. Instead, the data-driven approaches of quantitative biology are an option, to make use of recent scientific progress, changing business models at the same time.
5 Recent scientific progress: options for the healthcare industry
Biological research of recent decades has brought out a number of remarkable achievements. It can be seen already today in science that future progress is coupled to data-driven methodologies of quantitative biology, described in the sections above. Healthcare systems and healthcare industry will have to integrate this kind of methodologies to be able to capture the full potential of the new achievements. Some important examples are given in the following.
Non-coding RNAs that are transcribed from the respective stretches of the genomic DNA, but not further translated into polypeptides exist in virtually all types of cells in all three domains (archaea, prokaryotes, eukaryotes) of biology. A special class of those endogenic RNAs, the micro-RNAs, have been shown to be involved in the regulation of gene expression (Morris, 2008). Being also part of an additional system of inter-cellular, inter-tissue, and inter-species communication, they are released, together with proteins, other types of RNA, and also DNA, in extracellular vesicles, which in turn can be internalized by other cells. The molecular load of such vesicles has been recognized as a source of useful biomarkers and diagnostics for many dysfunctional phenomena and disease states (Mack, 2007) (Wang, et al., 2016).
A special class of small non-coding RNAs are the small inductive RNAs (siRNAs) (Zamore et al., 2000) (Ivanova et al., 2006). In contrast to the microRNAs they are double-stranded and exogenic. In the hands of molecular biologists, they serve as an important possibility for handling and controlling living cells, e.g. stem cells. They too, are a means of controlling gene expression, and probably will belong to new therapeutic tool boxes for future therapeutic concepts in molecular and systems medicine (Wittrup and Lieberman, 2015).
Another important achievement is the possibility to analyze single cells (Wang and Bodovitz, 2010) (Grün and van Oudenaarden, 2015)(Wang and Navin, 2015), comprising genomics, transcriptomics, proteomics, and metabolomics at single cell resolution. Though the majority of applications is in cancer research and has provided deep insight into the cancer genome and tumor development (Zhang et al., 2016), there are also applications in neurolo- gy and microbiome research. Altogether, this gives a new perspective for the meaning of precision or evidence-based medicine (Harz, 2017).
The ability, to induce pluripotent human stem cells from adult human skin cells (Takahashi et al., 2007) has opened up entirely new and ethically acceptable perspectives for regenerative medicine (Kang et al., 2016). This has to be seen also against the background of the status of synthetic biology (Cameron et al., 2014), which is about to become an important factor in the synthesis of drugs (Paddon and Keasling, 2014). In addition, particular applications for the medical sector begin to show promising results in diagnostics (Slomovic et al., 2015), the treatment of infectious diseases by bacteriophages and the treatment of cancer by means of engineered bacteria (Ruder et al., 2011), and the use of engineered bacteria (Zhou, 2016) and blood cells (Alapan et al., 2018) as drug carriers.
The spectacular accomplishment of utilizing the prokaryotic immune system for genome edit- ing by means of the CRISPR-Cas9 system and comparable systems (Garrett et al., 2011) (Gaj et al., 2013) (Lee et al., 2018) (Behler et al., 2018), is a breakthrough for synthetic biology and likely to induce a substantial change of paradigm in the future of healthcare. The possibility of directly curing genetic diseases appears in a new light. Not disregarding safety and ethical issues, one has to note that genome editing is about to bring therapeutic interventions to a new level that is likely to reduce the duration of treatments drastically. This should be kept in mind, when talking about the cost of medical genome editing.
The consequent advancement of using large biomolecules for therapeutic purposes is the employment of patients’ own modified cells, which is another application of synthetic biology. In the future, autologous stem or progenitor cells, modified by genome editing will be used to treat cancer, genetic diseases, and retroviral infections. Such therapeutic cells are an example of what is called advanced therapy medical products (ATMP) (Hanna et al., 2016). Of course, several hurdles still have to be surmounted. One of them is given by the situation that programming of autologous cells has to be done in a near-patient setting, which typically does not meet GMP requirements and hence will need special attention and care of regulatory agencies (Maciulaitis et al., 2012).
On the other hand, production and routine application of ATMPs requires personnel with new qualifications, different from current medical and health-care educational profiles. It can be expected that there will be a new kind of industry, let’s call it the “advanced therapeutic industry”, which will be manufacturer and service provider at the same time. Due to the complexity of the related liability situation, it is not very likely that the traditional “big pharma” industry will be directly involved in this kind of healthcare business.
It is easy to imagine that the new scientific and technological trends, based on data-driven methods, need special expertise. The data scientist will have a key function in future developments (Marx, 2013), be it in a scientific or a commercial environment. Of course, there will be different “flavors” depending on the origin and type of data. Accordingly, besides the qualification in computer science, statistics, and mathematics, data scientists will need further training in the fields of origin of the data. Universities are required to pave the way defining and configuring the respective curricula.
In summary, modern methods and technologies, which have found their way into the life sciences enable to look at living systems with an unprecedented resolution at atomistic, molecular, meso-, and macroscales. At the same time, gigantic amounts of data are generated and need careful data-driven analysis, to really capture the value of these data and to augment knowledge and understanding. For the future, this will be a sound basis for commercial exploitation of the new methodologies and technologies. Let me conclude with a statement by Nobel laureate Richard Feynman who said: “People who wish to analyze nature without using mathematics must settle for a reduced understanding.”
References
Abdulkader A, Lakshmirastan A, Zhang J (2016): Introducing DeepText: Facebook’s text understanding engine, available at https://code.facebook.com/posts/181565595577955/introducing-deeptext-facebook-s-text-understanding-engine/, accessed 21 May 2018.
Abu-Asab M, Chaouchi M, Alesci S, Galli S, Laassri M, Cheema A, Atouf F, VanMeter J, Amri H (2011): Biomarkers in the Age of Omics: Time for a Systems Biology Approach, OMICS, 15, p. 105-112.
Adams M (2013): Open questions: genomics and how far we haven’t come, BMC Biology, 11, 109.
Alapan Y, Yasa O, Schauer O, Giltinan J, Tabak A, Sourjik V, Sitti M (2018): Soft erythrocyte-based bacterial microswimmers for cargo delivery, Science Robotics, 3, eaar4423.
Altschul S, Gish W, Miller W, Myers E, Lipman D (1990): Basic Local Alignment Search Tool, Journal of Molecular Biology, 215, p. 403-410.
Altschul S (1991): Amino acid substitution matrices from an information theoretical perspective, Journal of Molecular Biology, 219, p. 555-565.
Ayers D, Day P (2015): Systems Medicine: The Application of Systems Biology Approaches for Mod- ern Medical Research and Drug Development, Molecular Biology International 2015, 698169.
Baldi P, Brunak S (2001): Bioinformatics – The Machine Learning Approach, MIT Press, Cambridge Mass. p.43-46.
Baldi P, Brunak S (2001b): Bioinformatics – The Machine Learning Approach, MIT Press, Cambridge Mass., p. 166-223.
Behler J, Sharma K, Reimann V, Wilde A, Urlaub H,HessW(2018):The host-encoded RNase Eendonuclease as the crRNA maturation enzyme in a CRISPR–Cas subtype III-Bv system, Nature Microbiology, 3, p. 367-377.
Berman H, Westbrook J, Feng Z, Gilliland G, Bhat T, Weissig H, Shindyalov I , Bourne P (2000): TheProtein Data Bank, Nucleic Acids Research, 28, p. 235- 242.
Bernardi G (2012): Fifty-Year Old and Still Ticking…. An Interview with Emile Zuckerkandl on the 50th Anniversary of the Molecular Clock, Journal of Molecular Evolution, 74, p. 233-236.
Bialek W, Botstein D (2004): Introductory Science and Mathematics Education for 21st-Century Biologists, Science, 303, p. 788-790.
Britton N (1986): Reaction Diffusion Equations and Their Applications to Biology, Academic Press, Burlington.
Caldwell G (2015): In silico tools used for compound selection during target-based drug discovery and development, Expert Opinion on Drug Discovery, 10, p. 901-923.
Cameron D, Bashor C, Collins J (2014): A brief history of synthetic biology, Nature Reviews Microbiology, 12, p.381-390.
Carbonell J, Michalski R, Mitchell T (1983): Machine Learning: A Historical and Methodological Analysis, AI Magazine, 4, p. 69-79.
Chara O, Tanaka E, Brusch L (2014): Mathematical Modeling of Regenerative Processes, in: Galliot B (ed.) Current Topics in Developmental Biology 108, Academic Press, Burlington p. 283-317.
Chow, M (2017): AI and machine learning get us one step closer to relevance at scale, available at https://www.thinkwithgoogle.com/marketing-resources/ai-personalized-marketing/, accessed 2018-05-10.
Christ B, Dahmen U, Herrmann K, König M, Reichenbach J, Ricken T, Schleicher J, Schwen J, Vlaic S, Waschinsky N (2017): Computational Modeling in Liver Surgery, Frontiers in Physiology, 8, 906.
Cornish-Bowden A (2013):The origins of enzyme kinetics, FEBS Letters, 587, p. 2725-2730.
Cornish-Bowden A (2015): One hundred years of Michaelis–Menten kinetics, Perspectives in Science, 4, p. 3–9.
Couzin J (2004): The New Math of Clinical Trials, Science, 303, p. 784-786.
Cunningham P (2010): The growing financial burden of health care: national and state trends, 2001-2006., Health Affairs, 29, p. 1037-1044.
de Ridder D, de Ridder J, Reinders M (2013): Pattern recognition in bioinformatics, Briefings in Bioinformatics, 14, p. 633-647.
Dickman S, Woolhandler S, Bor J, McCormick D, H. Bor D, Himmelstein D (2016): Health Spending For Low-, Middle-, And High-Income Americans, 1963–2012, HealthAffairs 35, p.1189-1196.
Dost F (1953): Grundlagen der Pharmakokinetik, Georg Thieme Verlag, Stuttgart.
Elsevier white paper (2017): Drug Attrition in Check: Shifting Information Input to Where it Matters, R&D Solutions for PHARMA & LIFE SCIENCES, Elsevier, Amsterdam.
Fagella D (2018): Machine Learning in Finance – Present and Future Applications, available at https://www.techemergence.com/machine-learning-in-finance/, accessed 2018-05-10.
Filippone M, Camastra F, Masulli F, Rovetta S (2008): A survey of kernel and spectral methods for clustering, Pattern Recognition, 41, p. 176-190.
Fitch W, Margoliash E (1967): Construction of Phylogenetic Trees, Science, 155, p. 279-284.
Frenkel D (1990): Monte Carlo Simulations. In: Catlow C, Parker S, Allen M (eds.) Computer Modelling of Fluids Polymers and Solids. NATO ASI Series (Series C: Mathematical and Physical Sciences), 293. Springer, Dordrecht.
Frey C (2012): Monitoring of complex industrial processes based on self-organizing maps and watershed transformations, Proceedings of the 2012 IEEE International Conference on Industrial Technology, IEEE, Piscataway, p. 1041-1046.
Friedman N (2004): Infering Cellular Networks Using Probabilistic Graphical Models, Science, 303, p. 799-805.
Frühbeis H, Klein R, Wallmeier H (1987): Computer-Assisted Molecular Design (CAMD) – An Overview, Angewandte Chemie Int. Ed. Engl., 26, p. 403-418.
Gaffney E, Monk N (2006): Gene Expression Time Delays and Turing Pattern Formation Systems, Bulletin of Mathematical biology, 68, p. 99-130.
Gaj T, Gersbach C, Barbas III C (2013): ZFN, TALEN, and CRISPR/Cas-based methods for genome engineering, Trends in Biotechnology, 31, p. 397-405.
Garrett R, Vestergaard G, Shah S (2011): Archaeal CRISPR-based immune systems: exchangeable functional modules, Trends in Microbiology, 19, p. 549- 556.
Green J, Hastings A, Arzberger P, Ayala F, Kottingham K, Cuddington K, Davis F, Dunne J, Fortin M, Gerber L, Neubert M, (2005): Complexity in Ecology and Conservation: Mathematical, Statistical, and Computational Challenges, BioScience, 55, p. 501-510.
Grün D, van Oudenaarden A (2015): Design and Analysis of Single-Cell Sequencing Experiments, Cell, 163, p. 799-810.
Gunawardena J (2014): Models in biology: ‘accurate descriptions of our pathetic thinking’, BMC Biology, 12, 29.
Gupta S (2012): Use of Bayesian statistics in drug development: Advantages and challenges, International Journal of Applied and Basic Medical Research, 2, p. 3-6.
Haken H, (1983): Synergetics – An Introduction, 3rd ed., Springer, Berlin.
Hanna E, Rémuzat C, Auquier P, Toumi M (2016): Advanced therapy medicinal products: current and future perspectives, Journal Health Policy and Market Access, 4, 31036.
Harz M (2017): Cancer, Computers and Complexity: Decision Making for the Patient, European Reviews, 25, p. 96-106.
Hastings A, Arzberger P, Bolker B, Ives T, Johnson N, Palmer M (2005): Quantitative Bioscience for the 21st Century , BioScience, 55 (6), p. 511–517.
Heffelfinger G, Martino A, Gorin A, Xu Y, Rintoul III M, Geist A, Al-Hashimi H, Davidson G, Faulon J, Frink L, Haaland D, Hart W, Jakobsson E, Lane T, Li M, Locascio P, Olken F, Olman V, Palenik B, Plimpton S, Roe D, Samatova N, Shah M, Shoshoni A, Strauss C, Thomas E, Timlin J, Xu D (2004): Carbon Sequestration in Synechococcus Sp.: From Molecular Machines to Hierarchical Modeling, OMICS: A Journal of Integrative Biology, 6, p. 305-330.
Henderson A, Korner-Bitensky N, Levin M, (2007): Virtual Reality in Stroke Rehabilitation: A Systematic Review of its Effectiveness for Upper Limb Motor Recovery, Topics in stroke Rehabilitation, 14, p. 52- 61.
Herculano-Houzel S (2009): The human brain in numbers: a linearly scaled-up primate brain, Frontiers in Human Neuroscience, 3, 31.
Hern, A (2016): ‘Partnership on AI’ formed by Google, Facebook, Amazon, IBM and Microsoft, available at https://www.theguardian.com/technology/2016/sep/28/google-facebook-amazon-ibm-microsoft-partnership-on-ai-tech-firms, accessed 21 May 2018.
Hoffmann R. (2009): Computer-Aided Synthesis Planning, in: Elements of Synthesis Planning, Springer, Berlin, p. 145-148.
Howard J (2014): Quantitative cell biology: the essential role of theory, Molecular Biology of the Cell, 25, p. 3438 – 3440.
Ideker T, Galitski T, Hood L, (2001): A New Approach to Decoding Life: Systems Biology, Annual Review of Genomics and Human Genetics, 2, p. 343-372.
Ivanova N, Dobrin R, Lu R, Kotenko I, Levorse J, DeCoste C, Schafer X, Lun Y, Lemischka I (2006): Dissecting self-renewal in stem cells with RNA interference, Nature, 442, p. 533-538.
Kaltenborn K, Rienhoff O (1993): Virtual Reality in Medicine, Methods of Information in Medicine, 32, p. 407-417.
Kang H, Shih Y, Nakasaki M, Kabra H, Varghese S (2016): Small molecule–driven direct conversion of human pluripotent stem cells into functional osteoblasts, Science Advances, 2, e1600691.
Karp P, Billington R, Caspi R, Fulcher C, Latendresse M, Kothari A, Keseler I, Krummenacker M, Midford P, Ong Q, Ong W, Paley S, Subhraveti P (2017): The BioCyc collection of microbial genomes and metabolic pathways, Briefings in Bioinformatics, bbx085, https://doi.org/10.1093/bib/bbx085.
Keseler I, Bonavides-Martínez C, Collado-Vides J, Gama-Castro S, Robert P. Gunsalus R, Johnson D, Krummenacker M, Nolan L, Paley S, Paulsen I, Peralta-Gil M, Santos-Zavaleta A, Shearer A, Karp P (2009): EcoCyc: A comprehensive view of Escherichia coli biology, Nucleic Acid Research, 37, p. D464-D470.
Koch C (2012): Modular Biological Complexity, Science, 337, p. 531-532.
Kohonen T (1958): Self-Organized Formation of Topologically Correct Feature Maps, Biological Cybernetics, 43, p. 59-69.
Kondo S, Miura T (2010): Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation, Science, 329, p. 1616-1620.
Kononenko I (2001): Machine learning for medical diagnosis: history, state of the art and perspective, Artificial Intelligence in Medicine, 23, p. 89-109.
Krieger E, Nabuurs S, Vriend G (2003): Introduction to homology modeling, Methods of Biochemical Analysis, 44, p. 509-523.
Krogh A, Brown M, Mian I, Sjölander K, Haussler D (1994): Hidden Markov Models in Computational Biology Applications to Protein Modeling, Journal of Molecular Biology, 235, p. 1501-1531.
Larkin M, Blackshields G, Brown N, Chenna R, McGettigan P, McWilliam H, Valentin F, Wallace I, Wilm A, Lopez R, Thompson J, Gibson T, Higgins D (2007): Clustal W and Clustal X version 2.0, Bioinformatics, 23, p. 2947-2948 (2007).
Laver K, George S, Thomas S, Deutsch J, Crotty M (2012): Cochrane review: virtual reality for stroke rehabilitation, European Journal of Physical and Rehabilitation Medicine, 48, p. 523-530.
Ledford H (2015): Team Science, Nature, 525, p. 308-311.
Lee H, Zhou Y, Taylor D, Sashital D (2018): Cas4- Dependent Prespacer Processing Ensures High-Fidelity Programming of CRISPR Arrays, Molecular Cell, 70, p. 1-12.
Lemoine F, Domelevo Entfellner J, Wilkinson E, Correia D, Dávila Felipe M, De Oliveira T, Gascuel O (2018): Renewing Felsenstein’s phylogenetic bootstrap in the era of big data, Nature, 556, p. 452-456.
Lennox B, Montague G, Frith A, Gent C, Bevan V (2001): Industrial application of neural networks – an investigation, Journal of Process Control, 11, p. 497-507.
Lenoir T (1999): Shaping Biomedicine as an Information Science, in: Bowden M, Bellardo Hahn T, Williams R (eds.), Proceedings of the 1998 Conference on the History and Heritage of Science Information Systems, ASIS Monograph Series, Information Today, Inc., Medford, NewJersey, p.27-45.
Leonard T, Hsu J (1999): Bayesian Methods – An Analysis for Statisticians and Interdisciplinary Researchers, Cambridge University Press, Cambridge UK.
Levin S (2006): Fundamental Questions in Biology, PLoS Biology, 4, e300.
Liu E (2010): Foundations for Systems Biomedicine: an Introduction, in: Liu E, Douglas A. Laufenburger D, (eds.), Systems Biomedicine – Concepts and Perspectives, Academic Press, Cambridge MA, p. 3-13.
Liu Z (2018): Towards precise reconstruction of gene regulatory networks by data integration, Quantitative Biology, https://doi.org/10.1007/s40484-018-0139-4
Luckow A, Cook M, Ashcraft N, Weill E, Djerekarov E, Vorster B (2017): Deep Learning in the Automotive Industry: Applications and Tools, arXiv:1705.00346v1 [cs.LG].
Lush J (1937): Animal Breeding Plans, Iowa State College Press, Ames, Iowa.
Maciulaitis R, D’Apote L, Buchanan A, Pioppo L, Schneider C (2012): Clinical Development of Advanced Therapy Medicinal Products in Europe: Evidence That Regulators Must Be Proactive, Molecular Therapy, 20, p. 479-482.
Mack, G (2007): MicroRNA gets down to business, Nature Biotechnology, 25, p. 631-638.
Mark C, Metzner C, Lautscham L, L. Strissel P, Strick R, Fabry B (2018): Bayesian model selection for complex dynamic systems, Nature Communications, 9, 1803.
Marshall W (2017): Introduction to Quantitative Cell Biology, Wallace F. Marshall, Editor, Morgan & Claypool, San Francisco.
Maurya M, Subramaniam S (2010): Computational Challenges in: Systems Biology, in: Liu E, Laufenburger D, (eds.), Systems Biomedicine – Concepts and Perspectives, Academic Press, London.
Marx V,(2013): Biology: The big challenges of big data, Nature, 498, p. 255-260.
MathWorks, Inc. (2018): How Machine Learning Works, available at https://www.mathworks.com/discovery/machine-learning.html#how-it-works, accessed 2018-05-10.
Mayer E, (1997): This is Biology – The Science of the Living World, Harvard University Press, Cambridge MA.
McCulloch W, Pitts W (1943): A logical Calculus of the Ideas Immanent in Nervous Activity, Bulletin of Mathematical Biophysics, 5, p. 115-133.
Michaelis L, Menten M (1913): Kinetik der Invertinwirkung, Biochemische Zeitung, 49, p. 333-369.
Morris, K (2008): in: Morris, K (ed.), RNA and the Regulation of Gene Expression – A Hidden Layer of Complexity, Caister Academic Press, Poole.
Musib M, Wang, F, Taraelli M, Yoho R, Yu K, Andrés R, Greenwald N, Pan X, Lee C, Zhang J, Dutton-Regester K, Johnston J, Sharafeldin I (2017): Artificial intelligence in research, Science, 357, p. 28-30.
Needleman S, Wunsch C (1970): A General Method Applicable to the Search for Similarities in the Amino Acid Sequence of Two Proteins, Journal of Molecular Biology, 48, p. 443-453.
Ollivier L (2008): Jay Lush: Reflections on the past, Lohmann Information, 43, p. 3-12.
Paddon C, Keasling J (2014): Semi-synthetic artemisinin: a model for the use of synthetic biology in pharmaceutical development, Nature Reviews Microbiology, 12, p. 355-367.
Pearson W, Lipman D (1988): Improved tools for biological sequence comparison, Proc. Natl. Acad. Sci. USA, 85, p. 2444-2448.
Pinto M, Martins P (2016): In search of lost time constants and of non-Michaelis—Menten parameters, Perspectives in Science, 9, p. 8-16.
PricewaterhouseCoopers (2009) Pharma 2020: Challenging business models, PWC International Ltd.
Radford A, Metz L, Chintala S (2016): Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, arXiv:1511.06434v2, 7 Jan 2016.
Rasmussen T, Krink T (2003): Improved Hidden Markov Model training for multiple sequence alignment by a particle swarm optimization—evolutionary algorithm hybrid, BioSystems, 72, p. 5-17.
Raue A, Schilling M, Bachmann J, Matteson A, Schelke M, Kaschek D, Hug S, Kreutz C, Harms B, Theis F, Klingmüller U, Timmer J (2013): Lessons Learned from Quantitative Dynamical Modeling in Systems Biology, PLoS ONE, 8, e74335.
RCSB PDB (2018): Research Collaboratory for Structural Bioinformatics, available at https://www. rcsb.org, accessed 2018-05-12.
Reitinger B, Bornik A, Beichel R, Schmalstieg D (2006): Liver Surgery Planning Using Virtual reality, IEEE Computer Graphics and Applications, 26, p. 36-47.
Reker D, Rodrigues T, Schneider P, Schneider G (2014): Identifying the macromolecular targets of de novo-designed chemical entities through self-organizing map consensus, Proc. Natl. Acad. Sci. USA, 111, p. 4067-4072.
Robertson M (2013): Open questions in biology – A tenth anniversary series, BMC Biology, 11, 7.
Romero P, Wagg J, Green M, Kaiser D, Krummenacker M, Karp P (2004): Computational prediction of human metabolic pathways from the complete human genome, Genome Biology, 6, R2.
Rosenblatt F (1958): The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain, Psychological Review, 65, p. 386- 408.
Ruder W, Lu T, Collins J (2011): Synthetic Biology Moving into the Clinic, Science, 333, p. 1248-1252.
Samuel A. (1959): Some studies in machine learning using the game of checkers. Recent Progress II, IBM Journal of Research and Development, 3, p. 535- 554.
Schneider G, Fechner U (2005): Computer-Based De Novo Design of Drug-Like Molecules, Nature Reviews Drug Discovery, 4, p. 649-662.
Shen D, Wu G, Suk H (2017): Deep Learning in Medical Image Analysis, Annual Review of Biomedical Engineering, 19, p. 221-248.
Schnell S, (2014): Validity of the Michaelis– Menten equation – steady-state or reactant stationary assumption: that is the question, FEBS Journal, 281, p. 464-472.
Schölkopf B, Smola A (2002): Learning with Kernels, MIT Press, Cambridge MA.
Sharan R, Ideker T (2006): Modeling cellular machinery through biological network comparison, Nature Biotechnolgy, 24, p. 427-433.
Sharkey K (2011): Deterministic epidemic models on contact networks: Correlations and unbiological terms, Theoretical Population Biology, 79, p. 115-129.
Shimizu K, Matsuoka Y (2015): Fundamentals of Modeling of Biosystems, in: Shimizu K, Matsuoka Y (eds.) Fundamentals of Systems Analysis and Modeling of Biosystems and Metabolism, Bentham Science Publishers Ltd., Sharja U.A.E., p. 81-132.
Siegel E, (2106): Predictive Analytics, Wiley, Hoboken.
Simula O, Vesanto J, Alhoniemi E, Hollmén J (1999): Analysis and Modeling of Complex Systems Using the Self-Organizing Map, in: Kasabov, Nikola, Kozma, Robert (Eds.), Neuro-Fuzzy Techniques for Intelligent Information Systems, Physica-Verlag, Heidelberg, pp. 3-22.
Slomovic S, Pardee K, Collins J (2015): Synthetic biology devices for in vitro and in vivo diagnostics, Proc. Natl. Acad. Sci. USA, 112, p. 14429–14435.
Smith T, Waterman M (1981): Identification of Common Molecular Subsequences, Journal of Molecular Biology, 147, p. 195-197.
Stansbury, D (2014): A Gentle Introduction to Artificial Neural Networks, available at https://the-clevermachine.wordpress.com/2014/09/11/a-gentle-introduction-to-artificial-neural-networks/, accessed 2018-05-12.
Stansbury, D (2014b): Error Backpropagation & Gradient Descent for Neural Networks, available at https://theclevermachine.wordpress. com/2014 /09/06/derivation-error-backpropagation-gradient-descent-for-neural-networks/, accessed 2018- 05-12.
Starruß J, de Back W, Brusch L, Deutsch A (2014): Morpheus: a user-friendly modeling environment for multiscale and multicellular systems biology, Bioinformatics, 30, p. 1331-1332.
Stergiopoulos Y, Kantaros Y, Tzes A (2012): Connectivity-aware coordination of robotic networks for area coverage optimization, Proceedings of the 2012 IEEE International Conference on Industrial Technology, IEEE, Piscataway, p. 31-35.
Takahashi K, Tanabe K, Ohnuki M, Narita M, Ichisaka T, Tomoda K, Yamanaka S (2007): Induction of Pluripotent Stem Cells from Adult Human Fibroblasts by Defined Factors, Cell, 131, p. 861-872.
Taylor D (2015):The Pharmaceutical Industry and the Future of Drug Development, in: Hester R, Harrison R (eds.), Pharmaceuticals in the Environment,
Royal Chemical Society, Cambridge UK, p. 1-33. Thakor R, Anaya N, Zhang Y, Vilanilam C, Siah K, Wong C, Lo A (2017): Just how good an investment is the biopharmaceutical sector?, Nature Biotechnology, 35, p. 1147-1157.
Ting D, Liu Y, Burlina P, Xu X, Bressler N, Wong T (2018): AI for medical imaging goes deep, Nature Medicine, 24, p. 534-540.
Tomita M, Hashimoto K, Takahashi K, Shimizu T, Matsuzaki Y, Miyoshi F, Saito K, Tanida S, Yugi K, Venter C, Hutchison III C (1999): E-CELL: software environment for whole-cell simulation, Bioinformatics, 15, p. 72-84.
Turing A (1952): The chemical basis of morphogenesis, Philosophical Transactions of the Royal Society London, B237, p.37–72.
Tyson B (2015): Why Pharma Must Change Its Model, Forbes Pharma & Healthcare, July 30, 2015, available at: https://www.forbes.com/sites/matthewherper/2015/07/30/why-pharma-must-change- its-model/2/#7dd1b84e3192, accessed 23 March 2018.
van der Meijden O, Schijven M (2009): The value of haptic feedback in conventional and robot-assisted minimal invasive surgery and virtual reality training: a current review, Surgical Endoscopy, 23, p. 1180–1190.
Venter C, Cohen D, (2004): The Century of Biol- ogy, New Perspectives Quarterly, 21, p. 73-77.
Visscher P, Hill W, Wray N, (2008): Heritability in the genomics era — concepts and misconceptions, Nature Reviews Genetics, 9, p. 255-266.
Vlachakis D, Bencurova E, Papangelopoulos N, Kossida S (2014): Current State-of-the-Art Molecular Dynamics Methods and Applications, in: Donev R (ed.), Advances in Protein chemistry and Structural Biology 94, Academic Press, Cambridge MA, p. 269-313.
Volpert V, Petrovskii S (2009): Reaction-diffusion waves in biology, Physics of Live Reviews, 6, p. 267-310.
Voosen P (2017): The AI Detectives, Science, 357, p. 22-27.
Wang G (2017): Global quantitative biology can illuminate ontological connections between diseases, Quantitative Biology, 5, p. 191–198.
Wang D, Bodovitz S (2010): Single cell analysis: the new frontier in ‘omics’, Trends in Biotechnology, 28, p. 281-290.
Wang J, Chen J, Sen S (2016): MicroRNA as Biomarkers and Diagnostics, Journal of Cellular Physiology, 231, p. 25-30.
Wang Y, Navin N (2015): Advances and Applications of Single-Cell Sequencing Technologies, Molecular Cell, 58, p. 598-609.
Windmann S, Eickmeyer J, Jungbluth F, Badinger J, Niggemann O (2016): Monitoring of Complex Industrial Processes based on Self-Organizing Maps and Watershed Transformations, in: Niggemann O, Beyerer J (eds.), Machine Learning for Cyber Physical Systems, Springer-Verlag, Berlin, p. 45-50.
Winslow R, Trayanova N, Geman D, Miller M (2012): Computational Medicine: Translating Models to Clinical Care, Science Translational Medicine 4, 158rv11.
Witkowski J, (2018): Cold Spring Harbor Symposium on quantitative Biology 1933: Surface Phenomena, available at http://symposium.csh lp.org/site/misc/topic1.xhtml, accessed 21 May 2018.
Wittrup A, Lieberman J (2015): Knocking down disease: a progress report on siRNA therapeutics, Nature Reviews Genetics, 16, p. 543-552.
Yuan H, Xiao S, Wang Q, WuK(2008): A Bioeconomic Model by Quantitative Biology to Estimate Swine Production. In: Li D (ed.) Computer And Computing Technologies In Agriculture, Volume I. CCTA 2007. The International Federation for Information Processing, vol 258. Springer, Boston, MA, p. 667- 675.
Zamore P, Tuschl T, Sharp P, Bartel D (2000): RNAi: Double-Stranded RNA Directs the ATP-Dependent Cleavage of mRNA at 21 to 23 Nucleotide Intervals, Cell, 101, p. 25-33.
Zanier E, Zoerle T, Di Lernia D, Riva G (2018): Virtual Reality for Traumatic Brain Injury, Frontiers in Neurology, 9, 345.
Zhang M, Tang C, (2013): QB: A new inter- and multi-disciplinary forum for modeling, engineer- ing and understanding life, Quantitative Biology 1, p. 1-2.
Zhang X, Marjani S, Hu Z, Weissman S, Pan X, Wu S (2016): Single-Cell Sequencing for Precise Cancer Research: Progress and Prospects, Cancer Research, 76, p. 1305-1312.
Zhou S (2016): Bacteria synchronized for drug delivery, Nature, 536, p. 33-34.
Zuckerkandl E, Pauling L (1962): Molecular disease, evolution, and genetic heterogeneity. In: M. Kasha, B. Pullman (eds.), Horizons in biochemistry, academic Press, New York, p. 189-225.
Zuckerkandl E, Pauling L (1962b): Evolutionary Divergence and Convergence in Proteins, in: Bryson V, Henry Vogel H (eds.), Evolving Genes and Proteins (New York: Academic Press, 1962), p. 97-166.
Zuckerkandl E, Pauling L (1965): Molecules as Documents of Evolutionary History, Journal of Theoretical Biology, 8, p. 357-366.